Содержание
Введение.
В первой части нашей статьи мы рассмотрели устройство трансформатора, принцип действия и виды трансформаторов. Теперь поговорим о них более детально.
Режимы работы трансформатора
Холостой ход однофазного трансформатора
Приведенные при рассмотрении принципа действии трансформатора соотношения справедливы лишь для идеального трансформатора, в котором пренебрегают сопротивлениями обмоток и потерями в сердечнике и считают, что магнитный поток замыкается только по сердечнику. В реальных условиях необходимо учитывать падения напряжения в обмотках и фактическую картину распределения магнитных полей. В частности, при холостом ходе МДС F0 кроме основного магнитного потока взаимоиндукции Ф0, замыкающегося по сердечнику, создает магнитный поток рассеяния Фрс1, который замыкается, в основном, по воздуху и сцепляется только с первичной обмоткой (рис. 1).
Рис. 1 — Холостой ход однофазного трансформатора
Под действием этого магнитного потока в первичной обмотке индуктируется ЭДС самоиндукции ерс1, действующее значение которой обычно рассчитывают по соотношению
где хрс1 — индуктивное сопротивление рассеяния первичной обмотки.
Для упрощения записи это сопротивление часто обозначают просто х1 Оно равно
где L1 — индуктивность рассеяния, определяемая по специальным формулам.
Таким образом, реально существующий магнитный поток рассеяния Фрс1 первичной обмотки и соответствующая ему ЭДС Ерс1 учитываются путем введения некоторого индуктивного сопротивления рассеяния х1, падение напряжения на котором уравновешивает ЭДС, т.е. в векторной форме равенство
записывают в виде
Такой подход значительно упрощает анализ и расчет режимов работы трансформатора. Сопротивление х1 практически постоянно, а величина Ерс1 пропорциональна току первичной обмотки.
Полное сопротивление первичной обмотки, кроме сопротивления х1 учитывает также активное сопротивление r1, т.е.
Электрическая схема замещения фазы первичной обмотки трансформатора на холостом ходу полностью аналогична схеме замещения катушки со стальным сердечником (рис. 2).
Рис. 2 — Электрическая схема замещения фазы трансформатора на холостом ходу
Уравнение электрического равновесия трансформатора для режима холостого хода может быть записано в виде
или
Таким образом, подводимое к первичной обмотке напряжение уравновешивается ЭДС самоиндукции Е10 и падением напряжения на сопротивлениях r1 и х1 обмотки. Поскольку падение напряжения достаточно мало, последнее уравнение для режима холостого хода часто записывают в виде
Векторная диаграмма трансформатора в режиме холостого хода является графической иллюстрацией и решением уравнений
Векторы 
как это следует из уравнений
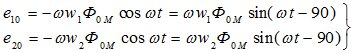
отстают от вектора Фом на 90° (рис.3). Величина напряжения U20 =Е20 отличается от Е10 в отношении коэффициента трансформации. Ток холостого хода I0 не синусоидален и его представляют в виде двух составляющих: I0а — активной, определяющей потери энергии в стали сердечника и в обмотке; I0р — реактивной, необходимой для создания МДС F0 и потоков Ф0 и Фрс1.
Рис. 3 — Векторная диаграмма холостого хода трансформатора
Таким образом, можно записать
Обычно I0а<< I0р и приближенно считают, что в режиме холостого хода ток I0, в основном, намагничивающий, т.е.
I0 ? I0р.
В целом вектор тока опережает вектор Фо на некоторый угол ?, называемый углом потерь
где rm и xm – активное и индуктивное сопротивления ветви намагничивания.
Следует отметить, что на рис. 3 векторы
показаны для наглядности в сильно увеличенном масштабе.
Работа трансформатора под нагрузкой
Нагрузочным или рабочим называется режим работы трансформатора, при котором к первичной обмотке подведено напряжение U1, а к вторичной подключены потребители ZН (рис. 4), так что I2 > 0.
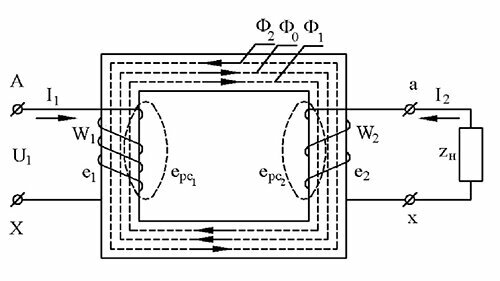
Рис. 4 — Нагрузочный режим однофазного трансформатора
Это основной режим, при котором вторичный ток изменяется в пределах 0<I2 ? I2Н , а коэффициент мощности cos?2 определяется характером нагрузки и может изменяться от нуля до 1,0. Особенности взаимодействий в рабочем режиме трансформатора определяются тем, что ток I2 создает МДС F2 = I2W2 и соответствующий магнитный поток Ф2, действующие встречно по отношению к МДС F1 и потоку Ф0, т.е. в соответствии с принципом Ленца реакция вторичной обмотки направлена на уменьшение основного магнитного потока взаимоиндукции Ф0, созданного при холостом ходе. Однако, поскольку подводимое к первичной обмотке напряжение не изменяется, а оно, в основном, уравновешивается ЭДС Е10, то поток Ф0 не должен изменяться, что соответствует уравнению равновесия:
Для поддержания неизменным магнитного потока при переходе от холостого хода трансформатора к нагрузке МДС I0W1 первичной обмотки увеличивается до такой величины I1W1, при которой компенсируется размагничивающее действие МДС вторичной обмотки I2W2. При этом закон Ома для магнитной цепи трансформатора в рабочем режиме записывается в виде:
Левые части соотношений одинаковы, поэтому справедливо равенство:
которое называют уравнением равновесия МДС трансформатора.
Из последнего равенства получают уравнения равновесия токов, которые записывают в виде:
или
При нагрузках, близких к номинальной, током холостого хода иногда пренебрегают и уравнение второе уравнение упрощается:
откуда следует соотношение:
Таким образом, соотношение токов при нагрузках, близких к номинальной, определяется соотношением числа витков, причем оно обратно пропорционально коэффициенту трансформации. Поэтому для номинального режима можно записать приближенное равенство:
из которого следует, что полная мощность, потребляемая трансформатором из сети, примерно равна полной мощности, отдаваемой потребителю.
Схема замещения первичной обмотки при переходе от режима холостого хода к нагрузке не изменяется, однако первичный ток увеличивается до значения I1 (рис.5, а), что должно найти отражение в уравнении равновесия ЭДС первичной обмотки при нагрузке:
Ток вторичной обмотки подобно току первичной обмотки создает магнитный поток рассеяния Фрс2, действие которого учитывается или величиной ЭДС самоиндукции Ерс2, или уравновешивающим ее падением напряжения I2x2, на индуктивном сопротивлении рассеяния
где L2 — индуктивность рассеяния вторичной обмотки.
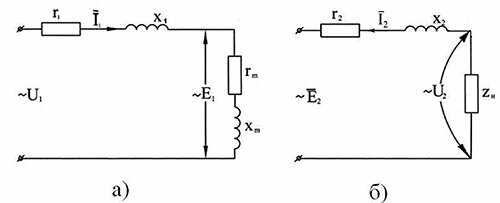
Рис. 5 — Схемы замещения первичной (а) и вторичной (б) обмоток трансформатора при нагрузке
Электрическая схема замещения вторичной обмотки показана на рис.5, б, на которой r2 — её активное сопротивление, а полное сопротивление нагрузки:
Уравнение электрического равновесия вторичной обмотки при нагрузке имеет вид:
Это уравнение источника электрической энергии, что и представляет собой трансформатор по отношению к нагрузке. Как видно, при работе под нагрузкой напряжение на нагрузке отличается от ЭДС Е2 на величину падения напряжения на внутренних сопротивлениях вторичной обмотки. Следует отметить, что соотношение между ЭДС Е2 и напряжением U2 зависит также от характера нагрузки, о чем будет сказано ниже.
Векторные диаграммы первичной и вторичной обмоток являются графическим решением уравнений:
Для вторичной обмотки (рис. 5, б) сдвиг по фазе между током I2 и напряжением U2 , (угол ?2) определяется соотношением параметров нагрузки:
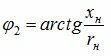
а угол ?2 — соотношением реактивных и активных сопротивлений вторичной обмотки и нагрузки, т.е.
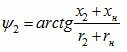
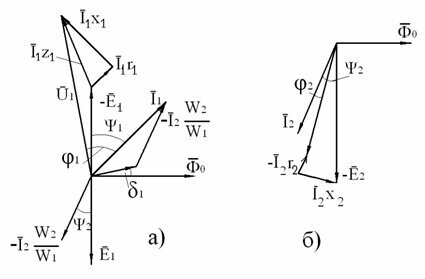
Рис. 6 — Векторные диаграммы первичной (а) и вторичной (б) обмоток трансформатора
На рис.6 векторные диаграммы изображены для случая активно-индуктивной нагрузки.На векторной диаграмме первичной обмотки (рис. 4, а) вектор тока 
получают, пристраивая к вектору тока холостого хода 
вектор тока 
измененный в отношении 1/к и повернутый на 180°, т.е. вектор
Построение вектора первичного напряжения U1 аналогично построению для режима холостого хода, однако векторы падений напряжения
ориентируются по отношению к вектору тока .
Сдвиг по фазе между током I1 и напряжением U1 обозначают ?1. Угол ?1, определяет, как известно, при заданных значениях тока и напряжения, подводимую к трансформатору от сети активную P1 = U1I1cos?1 и реактивную Q1 = U1I1sin?1 мощности. Чем больше угол ?1, тем меньше активная и тем больше реактивная мощности.
Режим короткого замыкания
Короткое замыкание (к.з.) трансформатора представляет собой такой режим его работы, когда вторичная обмотка замкнута накоротко (Zн = 0) и, следовательно, вторичное напряжение U2 равно нулю.
При внезапном коротком замыкании, когда к первичной обмотке подводится номинальное напряжение, токи в обмотках превышают номинальные значения в 10…20 раз. Такое к.з. может иметь место при эксплуатации трансформатора и является аварийным. Возникают недопустимые перегревы обмоток и значительные электродинамические усилия, которые приводят к разрушению трансформатора. Для защиты трансформатора от коротких замыканий применяются быстродействующие автоматы защиты.
В процессе испытания трансформаторов производят опыт короткого замыкания, но при таком пониженном первичном напряжении, чтобы токи в обмотках были равны номинальным. Это напряжение, выраженное в % от номинального (uк %), заносится на заводскую табличку трансформатора. Измерения при таком испытательном коротком замыкании, также как и измерения при холостом ходе позволяют определить ряд важных параметров трансформатора.
Приведенный трансформатор
Приведение вторичной обмотки трансформатора к первичной
Для упрощения анализа и расчета режимов работы трансформатора пользуются способом, при котором одна из его обмоток приводится к другой. Смысл приведения состоит в том, чтобы сделать ЭДС первичной и вторичной обмоток одинаковыми, электромагнитную связь между обмотками заменить электрической связью и получить единую электрическую схему замещения трансформатора, построить другую, более простую и наглядную векторную диаграмму. Чаще всего вторичную обмотку приводят к первичной. Для этого условно заменяют реальную вторичную обмотку некоторой фиктивной обмоткой с числом витков:
т.е. увеличивают число ее витков в k раз. Таким образом, коэффициент приведения вторичной обмотки к первичной равен коэффициенту трансформации. Все параметры приведенной обмотки обозначают со штрихами:
и т.д. В приведенной обмотке в соответствии с новым числом витков увеличиваются все ЭДС, напряжения и падения напряжения, т.е.:
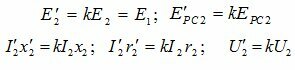
Важным условием приведения является то, чтобы мощности и потери энергии во вторичной обмотке не изменялись. Для этого должны выполняться равенства:
из которых получаются соотношения для тока и активного сопротивления приведенной вторичной обмотки:
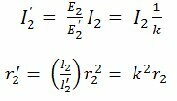
Аналогично последнему соотношению изменяются индуктивное сопротивление рассеяния приведенной вторичной обмотки и параметры нагрузки:
Для полных сопротивлений справедливы соотношения:
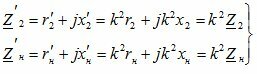
Если таким образом изменить (условно конечно) все электрические величины вторичной обмотки, то энергетические соотношения в реальном и приведенном трансформаторе сохраняются без изменений и поэтому приведение правомерно. При этом необходимо помнить, что приведение — это чисто аналитический прием, позволяющий упростить расчеты и анализ физических процессов в реальном трансформаторе.
Схема замещения и уравнения электрического равновесия приведенного трансформатора
Поскольку в приведенной вторичной обмотке ЭДС
равна ЭДС E1, то оказывается возможным схемы замещения первичной обмотки (рис. 5,а) и вторичной обмотки (рис. 5,б) с измененными параметрами объединить в одну схему замещения, соединив электрически точки равного потенциала. Такая полная двухконтурная схема замещения показана на рис. 7. Ее часто называют Т-образной схемой замещения приведенного трансформатора.
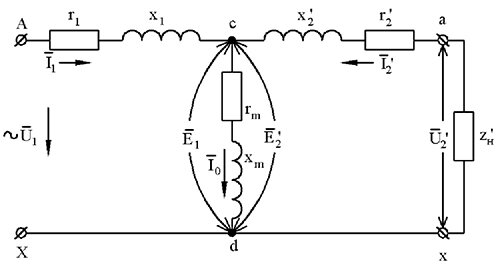
Рис. 7 — Т-образная схема замещения приведенного трансформатора
На этой схеме ветвь c – d с сопротивлениями rm и xm и током I0 называют ветвью намагничивания, ветвь А – с с током I1 — первичной ветвью, ветвь с – а– х – d с током 
— вторичной ветвью или вторичным контуром.Параметры схемы имеют строго определенные наименования: rm — активное сопротивление ветви намагничивания, учитывающее потери в стали магнитопровода на перемагничивание и вихревые токи:
— индуктивное сопротивление взаимоиндукции (ветви намагничивания).
Величина:
поэтому принимают, что:
r1 и r2’ — активные сопротивления первичной и приведенной вторичной обмоток; x1 и x2‘ — индуктивные сопротивления рассеяния первичной и приведенной вторичной обмоток;
— приведенное сопротивление нагрузки. Уравнения равновесия токов и ЭДС приведенного трансформатора записываются на основании 1 и 2 законов Кирхгофа:
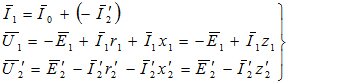
Полная векторная диаграмма приведенного трансформатора (рис.8) является графическим решением приведенных уравнений электрического равновесия.
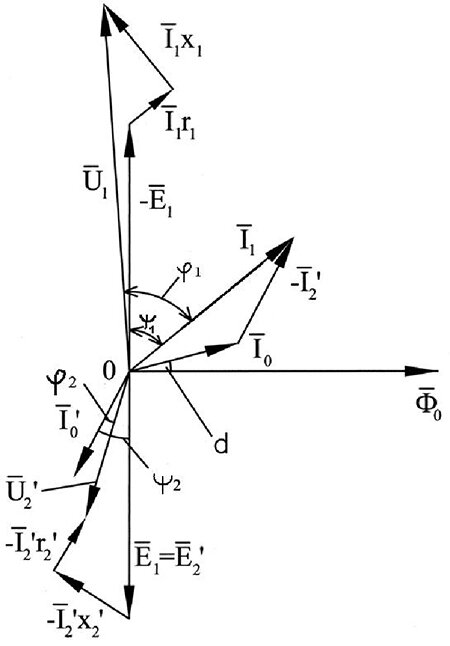
Рис. 8 — Векторная диаграмма приведенного трансформатора
Она объединяет векторные диаграммы первичной и вторичной обмоток, показанные на рис. 6 , при этом векторы ЭДС
и
между собой, а все построения для вторичной обмотки производятся для приведенных параметров.
Как отмечалось выше, в режимах номинальной нагрузки ток холостого хода I0 очень мал по сравнению с током I1н. Тем более он несоизмеримо мал по сравнению с током короткого замыкания, поэтому в этих режимах им можно пренебречь и в расчетах пользоваться упрощенной схемой замещения (рис. 9).
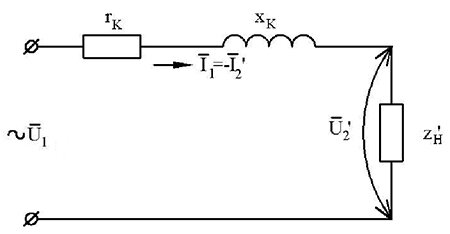
Рис. 9 — Упрощенная схема замещения приведенного трансформатора
Сопротивления rk = r1 +r2‘ и xk= x1 + x2называют сопротивлениями короткого замыкаия.
Уравнения электрического равновесия для упрощенной схемы имеют вид:
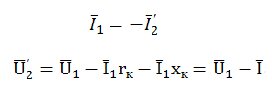
Опытное определение параметров схемы замещения трансформатора
Для определения параметров схемы замещения трансформатора проводят его испытания в режиме холостого хода и опытного короткого замыкания.
Схема опыта холостого хода приведена на рис.10 . Первичную обмотку подключают на номинальное напряжение и измеряют ток холостого хода I0 , мощность P0, напряжение на разомкнутой вторичной обмотке U20 .
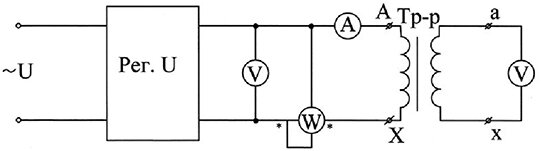
Рис. 10 — Схема опыта холостого хода
Мощность P0, потребляемая из сети, расходуется на потери в меди ?Pm1 = I02r1 и потери в стали ?Pст= I02rm при этом, поскольку rm»r1, потерями в первичной обмотке ?Pm1 пренебрегают и считают, что вся потребляемая из сети мощность расходуется на потери в стали, т.е.:
откуда:
Исходя из схемы замещения (рис. 5, а ) и пренебрегая величиной z1 по сравнению с zm можно определить величину zm из соотношения:
откуда:
Коэффициент мощности при холостом ходе определяется из соотношения:
Коэффициент трансформации равен:
Схема опыта короткого замыкания приведена на рис. 11.
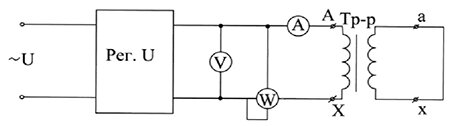
Рис. 11 — Схема опыта короткого замыкания
В этом опыте вторичная обмотка замыкается накоротко, а на первичной обмотке с помощью регулятора устанавливают такое напряжение U1k, при котором ток в первичной обмотке равен номинальному I1k = I1н. Величина U1k имеет весьма важное эксплуатационное значение и всегда указывается на щитке трансформатора. Обычно она указывается в процентах от номинального напряжения и для однофазных трансформаторов составляет 3%…5%.
Поскольку в рассматриваемом режиме U2=0, то трансформатор не отдает потребителю полезной мощности и вся мощность P1k, потребляемая из сети, расходуется на потери. Т.к. потери в стали ?Рст пропорциональны квадрату магнитной индукции ?Рст ? В2 ? Е2 ? U12, то, ввиду малости напряжения U1k, этими потерями пренебрегают и считают, что вся потребляемая мощность расходуется на потери в обмотках, т. е:
откуда получаем:
Полное сопротивление короткого замыкания равно:
поэтому :
Принимая далее, что :
получаем все параметры Т-образной схемы замещения трансформатора.
Рабочие характеристики трансформатора
Зависимость вторичного напряжения трансформатора от величины и характера нагрузки
Изменением напряжения двухобмоточного трансформатора при заданной нагрузке называется выраженная в процентах от номинального вторичного напряжения разность:
где U2o и U2н — вторичные напряжения при холостом ходе и при нагрузке.
Существуют определенные ГОСТом допустимые нормы изменения напряжения трансформатора при номинальной нагрузке. Часто в конструкции трансформатора предусматривается возможность в небольших пределах регулировать вторичное напряжение путем изменения числа витков первичной или вторичной обмоток, имеющих дополнительные выводы.
Физически влияние величины нагрузки на вторичное напряжение объясняется изменением (увеличением) падения напряжения на сопротивлениях обмоток трансформатора при увеличении тока нагрузки I2 (или I2’).
Логическая цепочка этого процесса такова:
При возрастании тока 
увеличивается и ток I1 вызывая увеличение падения напряжения в сопротивлениях первичной обмотки. Поскольку:
то это приводит к некоторому снижению ЭДС E1, и соответствующему изменению магнитного потока взаимоиндукции, а это влечет за собой уменьшение 
. В свою очередь падение напряжения на сопротивлениях вторичной обмотки создают дополнительные изменения напряжения 
.
Влияние характера нагрузки (отношения xн /rн) на величину вторичного напряжения при неизменном токе нагрузки удобно проследить, пользуясь упрощенной векторной диаграммой (рис. 1), на которой показаны режимы работы трансформатора для случаев ?2 > 0, ?2 = 0 и ?2 < 0, а также геометрическое место концов вектора 
при изменении угла ?2 пределах :
Построение упрощенных диаграмм производятся следующим образом: из точки 0 как из центра проводится дуга окружности радиусом, равным в принятом масштабе величине напряжения 
; под углом ?2 проводятся направления вектора вторичного напряжения 
; во всех случаях нагрузки треугольник короткого замыкания располагается таким образом, чтобы вершина А была на дуге , вершина С — на направлении вектора ; а катет ВС совпадал с направлением вектора тока 
.
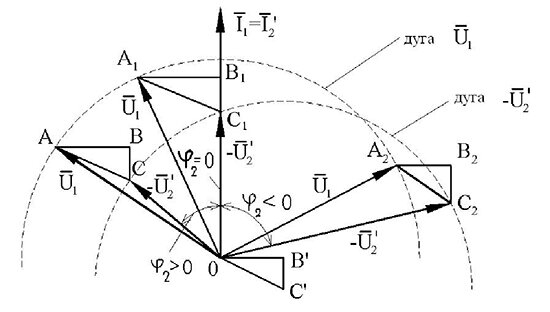
Рис. — 12. Упрощенная векторная диаграмма приведенного трансформатора при различных по характеру нагрузках
Точки С, С1 и C2 определяют величину приведенного вторичного напряжения при соответствующем значении ?2 . Если треугольник ABC поместить в положение 0 B’ C’, то дуга, проведенная из вершины С радиусом, равным , пройдет через точки С, С1 и C2 и является, таким образом, геометрическим местом конца вектора напряжения .Из рис. 12 хорошо видно, что при активно-индуктивной (?2 > 0) и чисто активной нагрузке (?2 = 0) приведенное вторичное напряжение меньше первичного напряжения 
.
При активно-емкостной нагрузке (?2 < 0) вторичное напряжение может стать даже больше первичного.
Физически это объясняется следующим образом. Реактивная мощность, необходимая для создания магнитного поля взаимоиндукции определяется, главным образом, реактивным сопротивлением рассеяния xk. При активно-емкостной нагрузке эта реактивная мощность может забираться от нагрузки и при определенной величине емкости в нагрузке избыток реактивной мощности отдается в первичную сеть. При этом растет ЭДС:
что приводит к перевозбуждению трансформатора, т.е. к возрастанию потока и увеличению напряжения .
Внешняя характеристика трансформатора
Внешней характеристикой трансформатора называют зависимость:
при 
и cos?1 = const (рис. 13).
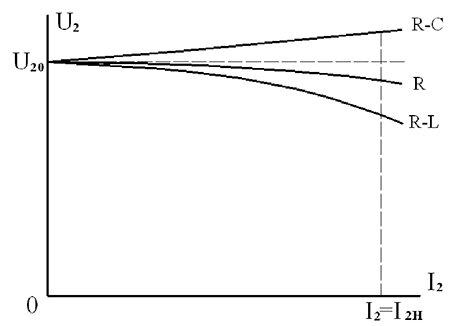
Рис. 13 — Внешняя характеристика трансформатора
Из рис. 13 следует, что внешняя характеристика трансформатора при увеличении тока нагрузки до номинального является достаточно жесткой. Изменение напряжения составляет всего несколько процентов и зависит от характера нагрузки, что находится в соответствии с векторной диаграммой (рис. 12 ).
При активной и активно-индуктивной нагрузке напряжение уменьшается, при активно-емкостной нагрузке оно может несколько возрастать. На практике величина изменения напряжения обычно рассчитывается по приближенной формуле:
где ? = I2/I2н нагрузка трансформатора в относительных единицах;
Потери в трансформаторе и его КПД
Трансформатор потребляет из сети мощность:
где m1 – число фаз.
Часть этой мощности, как отмечалось, теряется в виде потерь в обмотках:
другая часть — в виде потерь в сердечнике на гистерезисе и вихревые токи.
Электромагнитная мощность:
передается во вторичную обмотку посредством магнитного поля.
Полезная мощность равна:
Потери в стали:
мало изменяются при изменении нагрузки и относятся к категории постоянных потерь. Потери в обмотках:
являются переменными т.к. изменяются при изменении тока. Коэффициент полезного действия трансформатора показывает соотношение между мощностью, которая передается из первичной обмотки во вторичную и обратно, и мощностью, которая преобразуется в тепло. КПД определяется по формуле:
КПД силовых трансформаторов обычно достигает 94…98%. Рассчитывают трансформаторы таким образом, чтобы КПД имел наибольшее значение при нагрузке ? = 0,5 – 0,7 от номинальной. Обычно трансформаторы работают с некоторой недогрузкой — в области максимального значения КПД рис. 14.
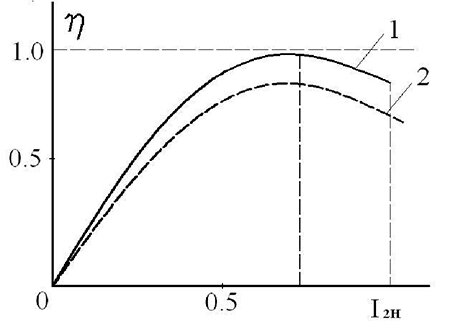
Рис. 14 — Коэффициент полезного действия трансформатора
При передаче значительной реактивной мощности (при уменьшении cos?2) КПД уменьшается, что показано на рис. 1, кривая 2.
Параллельная работа трансформаторов
Параллельная работа трансформаторов возможна лишь в том случае, если в обмотках трансформаторов не возникают уравнительные токи, а нагрузка распределяется пропорционально номинальным мощностям трансформаторов. Практически это сводится к выполнению следующих условий:
1. Напряжения обмоток высшего и низшего напряжения, указанные на заводских табличках, должны быть соответственно равны, т.е. должны быть равны коэффициенты трансформации k1 = k2 …kn.
2. Напряжения короткого замыкания uк, указываемые на заводских табличках трансформаторов, должны быть также равны; при параллельной работе трансформаторов допускают отклонения в пределах ±10 %.
3. Мощности параллельно работающих трансформаторов не должны значительно отличаться одна от другой. Допускается различие мощностей не больше чем в 3 раза.
4. Схемы и группы соединений обмоток трансформаторов, предназначенных для параллельной работы, должны быть одинаковыми. Это требование может быть выполнено, если условные обозначения схем и групп соединений, указанные на заводских табличках, будут одинаковыми.
5. Обмотки фаз трансформаторов, включенных для параллельной работы, должны совпадать, т. е. одинаково обозначенные выводы обмоток фаз должны быть присоединены к одной, а не к разным шинам.
Рассмотрим последствия нарушения названных условий.
Допустим, что не выполнено первое условие (k1 < k2 ). Это значит, что при одном и том же напряжении на первичных обмотках трансформаторов U1, вторичные ЭДС трансформаторов будут неодинаковы Е1 > Е2. Под действием возникшей разности потенциалов в замкнутом контуре вторичных обмоток пойдет уравнительный ток, который создаст падение напряжения в обмотках. В трансформаторе 1 это вызовет уменьшение напряжения на зажимах вторичной обмотки, в трансформаторе 2 – увеличение вторичного напряжения. В результате напряжение на внешних шинах будет иметь среднее значение. При нагрузке уравнительный ток накладывается на ток нагрузки, вследствии чего трансформатор 1 будет перегружен, а трансформатор 2 – недогружен. ГОСТ допускает расхождение в коэффициентах трансформации не больше ±0,5% от их среднего значения.
Если трансформаторы имеют неодинаковые номинальные напряжения короткого замыкания u1К ? u2К, значит неодинаковы сопротивления короткого замыкания Z1К ? Z2К. При работе трансформаторов в параллель напряжения вторичных обмоток одинаковы т. е. I12Z1К = I22Z2К, а это возможно лишь при неодинаковых токах трансформаторов. Это значит, что при параллельной работе трансформаторов нагрузка между ними будет распределяться непропорционально их номинальным мощностям. Чтобы не вызвать аварии трансформатора, имеющего меньшее значение uК, необходимо снижать общую нагрузку. Это ведет к неполному использованию трансформаторов. Согласно ГОСТ необходимо, чтобы разница напряжений короткого замыкания не превышала ±10% от их среднего значения, а соотношение номинальных мощностей параллельно работающих трансформаторов было не больше, чем 3:1.
Несоблюдение четвертого условия вызывает настолько большой уравнительный ток, что трансформаторы могут выйти из строя из-за перегрева обмоток. Даже при минимальном расхождении групп соединения трансформаторов (например, у одного группа ?/? – 0, а у другого ?/? – 11) уравнительный ток будет примерно в 5 раз больше номинального, что равносильно короткому замыканию.
Во избежание ошибок присоединение трансформаторов к сети без нулевого провода ( пятое условие ) производят следующим образом. Включают оба трансформатора со стороны высшего напряжения, затем один из них присоединяют к шинам низкого напряжения выводами обмоток всех фаз, а другой — выводами обмотки одной фазы, например С. Затем между выводами обмоток фаз В и А второго трансформатора и шинами низкого напряжения, к которым соответственно присоединены выводы обмоток фаз В и А первого трансформатора, включают вольтметр или лампу. Если обозначения выводов обмоток фаз на трансформаторах нанесены правильно, то между всеми парами одноименных выводов напряжение равно нулю (лампа не горит или вольтметр показывает нуль) и выводы В и А второго трансформатора могут быть соединены с шинами, к которым соответственно присоединены выводы В и А первого трансформатора.
Контрольные лампы или вольтметры при указанной проверке должны быть взяты на двойное рабочее напряжение трансформатора со стороны низшего напряжения.
