Важнейшими частями радиопередатчиков и радиоприемников являются колебательные контуры, в которых возбуждаются электрические колебания, т. е. переменные токи высокой частоты.
Для более ясного представления о работе колебательных контуров рассмотрим сначала механические колебания маятника (рис.1).
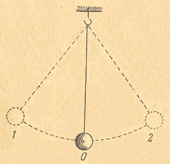
Если ему сообщить некоторый запас энергии, например толкнуть его или отвести в сторону и отпустить, то он будет совершать колебания. Такие колебания происходят без участия внешних сил только благодаря начальному запасу энергии, и поэтому называются свободными колебаниями.
Движение маятника из положения 1 в положение 2 и обратно является одним колебанием. После первого колебания следует второе, затем третье, четвертое и т. д.
Наибольшее отклонение маятника от положения 0 называется амплитудой колебания. Время одного полного колебания называется периодом и обозначается буквой Т. Число колебаний в одну секунду есть частота f. Период измеряется в секундах, а частота в герцах (гц). Свободные колебания маятника имеют следующие свойства:
1). Они всегда являются затухающими, т.е. амплитуда их постепенно уменьшается (затухает) вследствие потерь энергии на преодоление сопротивления воздуха и на трение в точке подвеса;
2). Свободные колебания можно считать гармоническими, т.е. синусоидальными, если не принимать во внимание их затухание;
3). Частота свободных колебаний маятника зависит от его длины и не зависит от амплитуды.При затухании колебаний амплитуда уменьшается, но период и частота остаются неизменными;
4). Амплитуда свободных колебаний зависит от начального запаса энергии. Чем сильнее толкнуть маятник или чем дальше отвести его от положения равновесия, тем больше амплитуда.
В процессе колебаний маятника потенциальная механическая энергия переходит в кинетическую и обратно. В положении 1 или 2 маятник останавливается и имеет наибольшую потенциальную энергию, а его кинетическая энергия равна нулю. По мере движения маятника к положению 0 скорость движения увеличивается и возрастает кинетическая энергия — энергия движения. При переходе маятника через положение 0 его скорость и кинетическая энергия имеют максимальное значение, а потенциальная энергия равна нулю. Далее скорость уменьшается и кинетическая энергия переходит в потенциальную. Если бы не было потерь энергии, то такой переход энергии из одного состояния в другое продолжался бы бесконечно и колебания были бы незатухающими. Однако практически всегда имеются потери энергии. Поэтому для создания незатухающих колебаний нужно подталкивать маятник, т.е. добавлять ему периодически энергию, возмещающую потери, как это делается, например, в часовом механизме.
Перейдем теперь к изучению электрических колебаний. Колебательный контур представляет собой замкнутую цепь, состоящую из катушки L и конденсатора С. На схеме (рис.2), такой контур образуется при положении 2 переключателя П. Каждый контур обладает еще и активным сопротивлением, влияние которого пока не будем рассматривать.
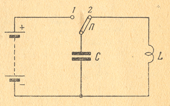
Назначение колебательного контура — создание электрических колебаний.
Если присоединить к катушке заряженный конденсатор, то его разряд будет иметь колебательный характер. Для заряда конденсатора надо в схеме (рис.2) поставить переключатель П в положение 1. Если затем его перевести на контакт 2, то конденсатор начнет разряжаться на катушку.
Процесс колебаний удобно проследить с помощью графика, показывающего изменения напряжения и и тока i (рис.3).
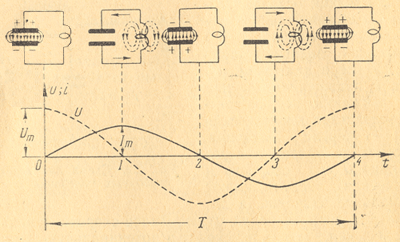
В начале конденсатор заряжен до наибольшей разности потенциалов Um, а ток I равен нулю. Как только конденсатор начинает разряжаться, возникает ток, который постепенно увеличивается На (рис.3) показано стрелками направление движения эчектронов этого тока. Быстрому изменению тока препятствует эдс самоиндукции катушки. По мере возрастания тока напряжение на конденсаторе уменьшается, в некоторый момент (момент 1 на рис.3) конденсатор полностью разрядится. Ток пристановится первоначальное состояние контура (момент 4 на рис.3).
Электроны в колебательном контуре совершили одно полное колебание, период которого показан на (рис.3) буквой Т. За этим колебанием следует второе, третье и т. д.
В контуре происходят свободные электрические колебания. Они совершаются самостоятельно без воздействия каких-либо внешних эдс, только благодаря начальному заряду конденсатора.
Эти колебания являются гармоническими, т. е. представляют собой синусоидальный переменный ток.
В процессе колебаний электроны не переходят с одной обкладки конденсатора на другую. Хотя скорость распространения тока очень велика (близка к 300 000 км/сек), электроны перемещаются в проводниках с весьма малой скоростью — доли сантиметра в секунду. За время одного полупериода электроны могут пройти только небольшой участок провода. Они уходят с обкладки, имеющей отрицательный заряд, в ближайший участок соединительного провода, а на другую обкладку приходят в таком же количестве электроны из участка провода, ближайшего к этой обкладке. Таким образом, в проводах контура совершается лишь смещение электронов на небольшое расстояние.
Заряженный конденсатор обладает запасом потенциальной электрической энергии, сосредоточенной в электрическом поле между обкладками. Движение электронов сопровождается возникновением магнитного поля. Поэтому кинетическая энергия движущихся электронов есть энергия магнитного поля.
Электрическое колебание в контуре представляет собой периодический переход потенциальной энергии электрического поля в кинетическую энергию магнитного поля и обратно.
В начальный момент вся энергия сосредоточена в электрическом поле заряженного конденсатора. Когда конденсатор разряжается, его энергия уменьшается и растет энергия магнитного поля катушки. При максимальном токе вся энергия контура сосредоточена в магнитном поле.
Дальше процесс идет обратным порядком: магнитная энергия уменьшается и возникает энергия электрического поля. Через полпериода после начала колебаний вся энергия опять сосредоточится в конденсаторе, а затем снова начнется переход энергии электрического поля в энергию магнитного поля и т. д.
Максимум тока (или магнитной энергии) соответствует нулю напряжения (или нулю электрической энергии) и наоборот, т. е. сдвиг фаз между напряжением и током равен четверти периода, или 90°. В первую и третью четверти периода конденсатор играет роль генератора, а катушка является приемником энергии. Во вторую и четвертую четверти, наоборот, катушка работает в качестве генератора, отдавая энергию обратно в конденсатор.
Особенностью контура является равенство индуктивного сопротивления катушки и емкостного сопротивления конденсатора для тока свободных колебаний. Это вытекает из следующего.
Конденсатор и катушка соединены своими зажимами друг с другом и поэтому напряжения на них равны. Ток I в катушке и конденсаторе один и тот же, так как контур представляет собой последовательную цепь. Поэтому можно написать
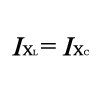
где ![]() — индуктивное сопротивление катушки, а
— индуктивное сопротивление катушки, а ![]() — емкостное сопротивление конденсатора.
— емкостное сопротивление конденсатора.
Разделив обе части этого равенства на I, получим
![]()
Значение индуктивного или емкостного сопротивления элементов контура на частоте собственных колебаний называют характеристическим (иногда волновым, что неудачно) сопротивлением контура и обозначают греческой буквой р (ро)
![]()
Величина ? обычно бывает порядка нескольких сотен ом.
